III. Les théories mathématico-musicales autour de la consonance
A. La théorie d’Euler: associer des degrés de douceur aux accords
En 1731, Euler écrit un essai sur la musique appelé Essai d'une nouvelle théorie de la musique, exposée en toute clarté selon les principes de l'harmonie les mieux fondés (Tentamen novae theoriae musicae ex certissimis harmoniae principiis dilucide expositae), dans lequel il expose sa théorie musicale. Elle ne sera publiée qu’en 1739, après avoir été modifiée tout au long de sa vie.
D’après Euler, un son est agréable car il témoigne d’un ordre. Soit l’ordre est connu, et il s’agit seulement d’une reconnaissance, soit il est inconnu et il faut le rechercher : ce dernier ordre concerne la musique. Il existe deux types d’ordres de sons : la hauteur (si un son est grave ou aigu) et la durée. Nous pouvons aussi admettre l’existence d’un ordre de son basé sur l’intensité, mais il dépend de la manière dont le musicien joue le morceau.
Euler reconnaît aussi que l’ordre de la hauteur est plus important que celui de la durée car celle-ci se mesure par la fréquence. Le mathématicien ramène alors l'évaluation du plaisir musical à la mesure des proportions attachées aux sons.
Ses idées ne sont pas tout à fait nouvelles, les Grecs anciens utilisaient l’idée de proportions et la théorie de Leibniz parlait déjà de perception inconsciente des rapports des fréquences sonores par notre oreille. Toutefois, Euler cherche à l’expliquer.
Tout d’abord, Euler définit une échelle de “bonté”. Pour cela, il reprend la théorie de la coïncidence des coups. Sachant que les coups d’une note correspondent à un niveau de pression, le temps écoulé entre deux coups successifs correspond à la période de l’onde sonore associée à la note, et le nombre de coups par unité de temps à la fréquence. La théorie dit qu’un intervalle est d'autant plus consonant que le temps entre deux coïncidences consécutives de coups est court. Autrement dit un intervalle est plus consonant si la fréquence de coups coïncidents est élevé (nombre de coups coïncidents par unité de temps).
Une note jouée seule, ou deux notes à l'unisson, donnent l'ordre le plus simple. Cela correspond à l’intervalle entre deux mêmes sons (1 et 1). Il répond au rapport et correspond au premier degré de douceur d’Euler. Puis, arrive l’octave (1 et 2) de rapport ; qui correspond au deuxième degré de douceur. Les rapports et correspondent à la quinte de l'octave supérieure et à la double octave et sont regroupés dans le 3e degré de douceur.
Euler attache ensuite le degré au rapport , c’est à dire qu’à chaque puissance de 2 est attaché le degré supérieur.
Cependant, Euler remarque que (qui correspond au rapport des fréquences de la sixte mineure 3 octaves en-dessous et qui ne correspond pas à une puissance de deux mais un nombre premier) doit être plus complexe que qui a le degré 4, Euler lui attribue donc le degré 5 et en déduit par induction que pour , un nombre premier, est de degré .
Puis, il essaie de généraliser en disant que le rapport "dépasse" celui de comme dépasse . Il faut donc que son degré soit composé de , et , ce qui donne le degré: .
Patrice Bailhache proposera en 1997 une autre approche pour obtenir . Si l’on prend un rapport avec et premiers entre eux, nous avons d’après la théorie de la coïncidence des coups, que seuls le premier et le dernier coups sont les mêmes (le coup en commun provient du fait qu’ils sont joués en même temps; et comme ils sont premiers entre eux, ils ne partagent pas d’autres coups en commun). En sachant que le dernier coup de la période correspond au début de la période d’après, le total des coups sera .
En généralisant, nous associons le rapport au degré avec des nombres premiers et des coefficients entiers positifs. Nous pouvons aussi remarquer que ces résultats ne sont pas vraiment rigoureux, mais les propriétés qu’Euler en déduit sont intéressantes.
En effet, cette formule peut s’appliquer à plus que 2 sons. Quatre sons dans les rapports avec , et premiers sont assimilés à . Si au contraire, ils ne sont pas premiers, et que l’on a par exemple: (avec , , et entiers), il suffit de prendre le de tous ces facteurs, soit , ce qui nous donne . Euler peut ainsi toujours se ramener au cas .
Si par contre, le rapport de 2 sons (ou plus) n’est pas de la forme mais comme la quinte de rapport , il faudra au préalable les diviser par le de ces nombres, et ensuite éventuellement appliquer le . Par exemple, deviendra .
La question de la consonance se réduit donc au calcul du degré de douceur de leur par la formule ci-dessus. Le tableau ci-dessous montre le classement des dans les 16 premiers degrés.
Dans une deuxième partie de l’essai, Euler fait une étude mathématique des harmoniques, dans lequel il justifie la consonance. Son étude se base sur le calcul du d’un accord, qu’il appelle exposant. Il obtient d’abord un classement des consonances représenté sur le tableau ci-dessous où les caractères gras représentent les rapports des consonances et ceux soulignés, aux dissonances traditionnelles:

Tableau 6.1: degrés de douceur avec leurs rapports correspondants
Puis, en prenant le tableau précédent et n’y laissant que les consonances et dissonances, nous retrouvons cette classification:
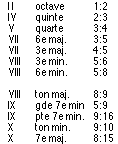
Tableau 6.2: les intervalles classiques avec leur degré de douceur correspondant
Or, elle correspond à une des classifications de Mersenne, un religieux mathématicien et philosophe du XVIIème. Ce dernier a écrit Harmonie universelle, contenant la théorie et la pratique de la musique, un ouvrage majeur du XVIIème siècle publié en 1636 et qui englobe tous les aspects de la musique de cette époque. Euler comme Mersenne met en avant l’idée que les dissonances ne sont que des consonances de degré élevé: il n’y a qu’une frontière floue entre les deux. Cette idée était donc répandue à l'époque d'Euler.
Mais Euler va plus loin. Il remarque que si l’on ajoute un ou plusieurs sons à un accord, de rapports correspondant à des diviseurs de l’exposant (l’exposant étant le ), son degré de douceur ne change pas. Par exemple, a le même exposant que et car ils ont le même , c’est à dire 6. Il définit alors l’accord dit complet comme un accord dont nous ne pouvons ajouter de sons sans que son degré n’augmente (c’est à dire sans que son n’augmente): cet accord contient donc tous les diviseurs de son exposant. Par exemple, est un accord complet. Pour Euler, un effet de plénitude est alors ressenti par l’oreille. C’est comme cela qu’il retrouve les accords les plus consonants de chaque degré.
Prenons l’exemple de l’accord parfait majeur de do composé du do, mi et du sol. Ces trois notes correspondent aux nombres 4, 5 et 6, de 60. L’accord complet associé sera alors composé de 12 notes, associées à , soit le do1, do2, sol2, do3, mi3, sol3, mi4, sol4, si4, mi5, si5 et si6. Euler prétend alors que cet accord complet est aussi doux que l’accord parfait majeur de do (do, mi et sol), alors qu’il s’étale sur 6 octaves et qu’il comprend la septième majeure (entre do et si).
On peut le justifier si l'on se réfère à la théorie moderne des sons partiels de Helmholtz. En produisant les sons do, mi et sol, cette théorie dit qu’on entend également d’autres fréquences de ces notes (ce qui inclue tous les intervalles obtenus à partir de la note) plus élevées (comme le do une octave plus haut): ce sont les partiels de ces notes. nous en reparlerons plus tard. Dans notre cas, nous entendrons entre autres le si à plusieurs reprises, soit en tant que quinte de mi, soit en tant que tierce majeure de sol. Toutefois, l’intensité de si4 si5 si6 ne sera que très faible.
![]()
Enregistrement de l'accord parfait majeur de do généré sur Audacity
![]()
Enregistrement de l'accord complet de l'accord parfait majeur de do généré sur Audacity
Autre exemple: si l’on ajoute un deuxième do (do2) à l’accord do, mi, et sol, nous aurons les coefficients 4, 5, 6 et 8 de 120. Nous sommes donc 1 degré plus haut, et l’accord complété se voit ajouté un si à la 7e octave.
En résumé, Euler définit la consonance à partir de la théorie de l’ordre et de la théorie de la coïncidence des coups. Il classe les accords à partir de leur rapport de fréquence: c’est le degré de douceur d’un accord. Si cet accord présente un rapport de la forme (différent de ), il faut au préalable le diviser par son . Si et ne sont pas premiers entre eux, il faut aussi le diviser par leur . Il définit aussi l’accord complet de sorte que si l’on ajoute un son à cet accord, son degré de douceur ne pourra qu’augmenter.
Euler n’est pas le seul à chercher à expliquer la musique. D’Alembert, un de ses contemporains en fait de même.
