La théorie de Helmholtz : quantifier la dissonance

     Afin d’expliquer la consonance, Helmholtz commence par étudier le fonctionnement de l’oreille, en se basant sur les observations de son époque. Cela constitue la première partie de sa Théorie physiologique de la musique publié en 1863. Il cherche ensuite à expliquer la consonance, c’est-à-dire pourquoi certains sons nous semblent plus agréables que d’autres. Pour cela, il se base sur le phénomène des battements : si les fréquences de deux sons sont voisines, alors nous entendons un battement, un son désagréable. D’un côté, plus l’écart entre les fréquences est grande, moins le battement est entendu, car il est trop lent pour être audible. Il en est de même si l’écart est trop petit, comme lorsqu’une image clignote très rapidement et apparaît comme continue. Il définit donc la consonance et la dissonance à partir de la présence ou l’absence de battements.

     Helmholtz cherche alors la fréquence qui est la plus désagréable (pour laquelle la dissonance est maximale), et retrouve la valeur de $30Hz$. Puis, il trouve une formule qui renvoie la “dureté propre” de deux sons simples en fonction de l’écart de leur fréquence (que l’on verra après). Cette dureté ne correspond pas à la dissonance, qui dépend en plus de l’énergie des battements. Helmholtz suppose que cette dépendance est linéaire : la dissonance est ainsi le produit de la dureté propre de deux sons simples par l’énergie des battements.

     Pour retrouver la dissonance de deux sons complexes, il suffit, d’après Fourier, de simplement additionner toutes les dissonances entre les harmoniques correspondants. Sachant que le timbre correspond au spectrogramme du son, ce résultat dépend donc du timbre du son, soit de l’instrument.

     On remarque que certains résultats de Helmholtz sont obtenus arbitrairement, ce qui montre la subjectivité de la consonance et de la dissonance.

     Helmholtz établit ensuite un graphique, sur lequel est basé sa théorie musicale, qui présente la dissonance de plusieurs notes (calculée à partir des 10 premiers partiels harmoniques du violon) en fonction de la note. Le voici:

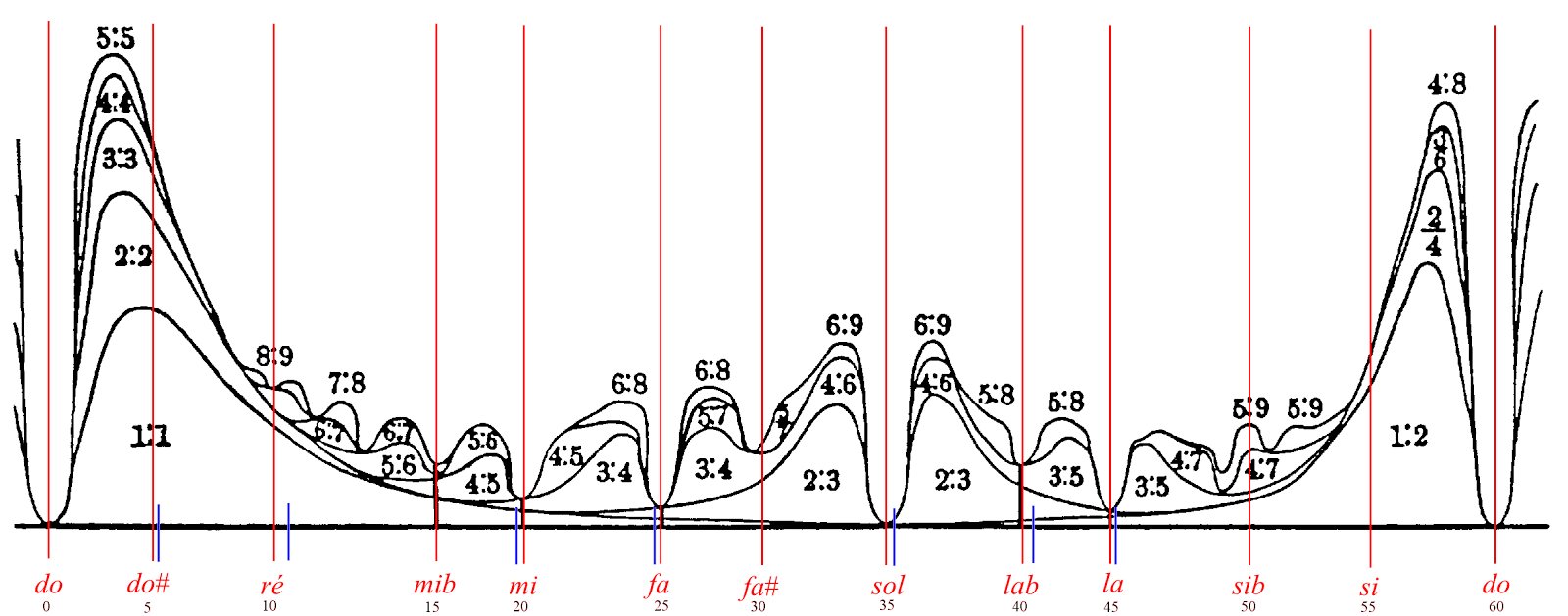
     Ce graphique est en accord avec les consonances déjà établies (elles ont des valeurs proches de 0): l’unisson (do), l’octave (do), la quinte (sol), la quarte (fa), la sixte majeure (la), la tierce majeure (mi), la tierce mineure (mib) et la sixte mineure (lab). Plus nous nous éloignons de ces intervalles, plus la dissonance croît rapidement. Cette théorie scientifique concorde donc avec le monde de la musique.

     Helmholtz parvient à ces résultats en plusieurs étapes. D’abord, il calcule l’énergie où les battements sont maximaux. Nous fixons $f_1$ la fréquence de référence par rapport à laquelle nous allons calculer la dissonance d’autres notes de fréquence $f$. Cela correspond au do dont la fréquence est $264Hz$ dans notre cas. L’écart des deux fréquences, $f - f_1 = f - 264$.

     Ensuite, Helmholtz choisit la fonction: $f(x)=(\frac{60x}{900+x^2})^2$pour calculer la dureté propre en notant toutefois que "c'est l'expression la plus simple qui remplisse les conditions données mais elle est naturellement arbitraire jusqu'à un certain point." Il a sûrement obtenu cette fonction en sachant que la dissonance était maximale en $30Hz$, et presque nulle lorsque la différence des fréquences est grande. Dans notre cas, x correspond à la différence de fréquences entre les deux sons, ce qui nous donne:

$D = \frac{3600*(f-264)^2}{(900+(f-264)^2)^2}$

     Et en multipliant l’énergie des battements ($E$) par $D$, nous obtenons la dissonance de deux sons simples. nous avons pour $f$ variant de$296$ à $396Hz$, (qui correspond à la courbe $1:1$ dans le graphique)

     Jusqu’à présent, nous avons étudié la dissonance de deux sons simples. Pour obtenir la dissonance de deux sons en dents de scie, ce qui correspond au timbre d’un instrument à cordes frottées, il faut maintenant additionner les partiels des deux sons concernés (Helmholtz prendra les 10 premiers harmoniques).

     Maintenant, lorsque l’on fait varier $f$ entre $264$ et $528$ ($=2*264$; puisque la note se retrouve entre le do et le do une octave au-dessus) nous pouvons remplacer $f$ par $f_1*k$ ($k$ varie entre 1 et 2 et correspond donc au rapport $f/f_1$), soit $264*k$. Nous pouvons calculer la dissonance entre deux harmoniques des deux sons (la $m_1$-ème du premier, de fréquence $264$, et la $m_2$-ème du second, de fréquence $f$) grâce à cette formule:

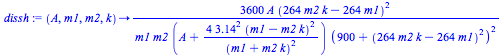
(où $3.14$ correspond à $\pi$, dissh la dissonance de deux partiels et $A$ est une constante)

     Pour $k$ variant de $1$ à $2$, et $m_1$ et $m_2$ variant de $1$ à $10$ chacun, car nous prendrons les 10 premiers harmoniques (et $A$ qui ici vaut $0.1$), nous obtenons graphiquement:

     La théorie de Helmholtz est fondée sur l’étude des battements. D’après lui, la dissonance entre deux sons simples est égale au produit de l’énergie des battements par la dureté propre de l’accord, la dureté propre étant obtenue à partir de l’écart de fréquences des deux sons. Pour obtenir la dissonance de deux sons complexes, il suffit d’additionner la dissonance de leurs harmoniques. Nous obtenons en même temps les accords consonants, car ils correspondent aux accords de dissonance faible.

     Nous avons ainsi vu comment trois scientifiques expliquent la consonance: Euler en associant des degrés de douceur aux rapports de fréquences justifiés par la coïncidence des coups; D’Alembert par des constats, et Helmholtz par les battements. Toutefois, leurs théories sont dans une certaine mesure arbitraires, car ils ne se fondent pas sur des hypothèses communément acceptées.